Teorema de Gauss-Bonnet generalizado

Teorema de Gauss-Bonnet generalizado: En matemáticas, el teorema de Gauss-Bonnet generalizado presenta la característica de Euler de una variedad de Riemann cerrada como integral de cierto polinomio derivado de su curvatura. Es una generalización directa del teorema de Gauss-Bonnet a la dimensión par en general. Sea M una variedad de Riemann compacta de la dimensión 2n y sea O la forma de curvatura de la conexión de Levi-Civita. Esto significa que O es 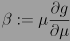-valorada en M. Tal O puede ser mirado como matriz anti-simétrica 2n×2n cuyas entradas sean 2-formas, así que es una matriz sobre el anillo conmutativo 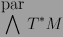. Uno puede por lo tanto tomar el Pfaffiano de O Pf(O) que resulta ser una 2n-forma.

Игры ⚽ Нужно решить контрольную?

Teorema de Gauss-Bonnet generalizado — En matemáticas, el teorema de Gauss Bonnet generalizado presenta la característica de Euler de una variedad de Riemann cerrada como integral de cierto polinomio derivado de su curvatura. Es una generalización directa del teorema de Gauss Bonnet a … Wikipedia Español
Teorema de Gauss-Bonnet — Un ejemplo de región compleja donde el teorema de Gauss Bonnet puede ser aplicado. Se muestra el signo de la curvatura geodésica. El teorema de Gauss Bonnet en geometría diferencial es una proposición importante sobre superficies que conecta su… … Wikipedia Español
Característica de Euler — Saltar a navegación, búsqueda En topología algebraica, la característica de Euler o característica de Euler Poincaré es un invariante topológico (de hecho, invariante homotópico) definido para una amplia clase de espacios topológicos. Es denotada … Wikipedia Español
Shiing-Shen Chern — 220px Nacimiento 26 de octubre de 1911 Jiaxing, Zhejiang,China Fallecimiento 3 de diciembre de 2004 Tianjin,China … Wikipedia Español
Clase característica — En matemáticas, una clase característica es un elemento del módulo de cohomología de un espacio topológico y que satisfacen ciertos axiomas considerando varias de ellas. Son un concepto unificador entre la topología algebraica, geometría… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico